引言

函数图像是数学和物理学中非常重要的概念，它能够直观地展示函数的性质和变化趋势。通过函数图像，我们可以更深入地理解函数的增减性、周期性、奇偶性等特性。本文将围绕函数图像专题，探讨函数图像的基本概念、绘制方法以及在实际应用中的重要性。

函数图像的基本概念

函数图像是函数在坐标系中的图形表示。通常，横轴表示自变量x，纵轴表示函数值y。每个x值对应一个y值，这些点在坐标系中连成一条曲线，就形成了函数的图像。函数图像可以帮助我们直观地了解函数的性质，例如单调性、奇偶性、周期性等。

函数图像的绘制方法

绘制函数图像通常遵循以下步骤：

• 确定函数的定义域和值域。

• 选择合适的坐标系。

• 根据函数的性质，确定关键点，如极值点、拐点、渐近线等。

• 绘制函数图像，连接关键点。

• 标注坐标轴、函数名称、关键点等。

  

常见函数的图像特点

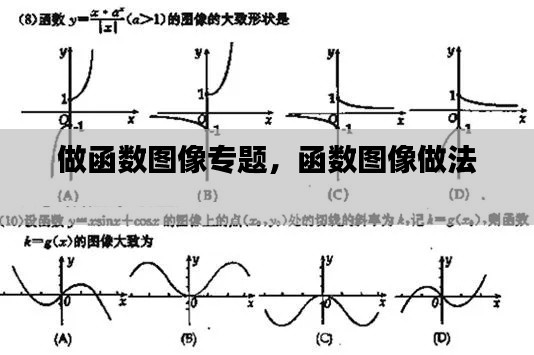
以下是一些常见函数的图像特点：

• 线性函数：图像是一条直线，斜率表示函数的增长速度。

• 二次函数：图像是一条抛物线，开口方向和顶点位置取决于二次项系数和一次项系数。

• 指数函数：图像呈指数增长或衰减，增长速度随自变量增加而加快或减慢。

• 对数函数：图像呈对数增长，增长速度随自变量增加而减慢。

• 三角函数：图像具有周期性，如正弦函数和余弦函数在[0, 2π]区间内重复。

函数图像的应用

函数图像在各个领域都有广泛的应用，以下是一些例子：

• 物理学：在物理学中，函数图像可以用来描述物体的运动轨迹、振动、电磁场等。

• 工程学：在工程学中，函数图像可以用来分析电路、控制系统、信号处理等问题。

  

• 经济学：在经济学中，函数图像可以用来表示需求、供给、价格等经济变量之间的关系。

• 生物学：在生物学中，函数图像可以用来描述种群增长、生物分布等。

函数图像的局限性

尽管函数图像在理解和分析函数方面非常有用，但它也存在一些局限性：

• 无法展示函数的局部性质，如导数和二阶导数。

• 对于复杂的函数，图像可能难以绘制和理解。

• 函数图像可能无法准确反映函数在无穷远处的行为。

结论

函数图像是数学和自然科学中不可或缺的工具，它能够帮助我们直观地理解函数的性质和变化趋势。通过学习和掌握函数图像的绘制方法，我们可以更好地应用于实际问题中，提高解决问题的能力。在未来的学习和工作中，我们应该重视函数图像的学习，不断拓展我们的数学视野。